Nghiệm thu đề tài cấp ĐHQG-HCM thuộc Chương trình Toán tại Trường Đại học Bách khoa: Các thuật toán hiệu quả tìm đường đi hình học có ràng buộc ngắn nhất trên mặt phẳng và ứng dụng trong robot
|
1. |
Tên đề tài: | Các thuật toán hiệu quả tìm đường đi hình học có ràng buộc ngắn nhất trên mặt phẳng và ứng dụng trong robot |
| 2. | Mã số | T2022-20-01 |
| 3. | Chủ nhiệm đề tài: |
PGS.TS Phan Thành An Nhóm nghiên cứu gồm: 2PGS.TS, 2TS, 2ThS và 1CN. |
| 4. | Đơn vị: | Trường Đại học Bách Khoa, ĐHQG-HCM |
| 5. | Lĩnh vực: | Toán học |
| 6. | Loại hình : | Nguyên cứu cơ bản |
| 7. | Thời gian thực hiện: |
24 tháng (2022-2024) |
| 8. | Kinh phí nghiên cứu: | 675 triệu đồng |
| 9 | Thời gian nghiệm thu | Ngày 11 tháng 12 năm 2023 |
| 10 | Chủ tịch Hội đồng và quyết định thành lập HĐ |
Quyết định 1639/QĐ-ĐHQG ngày 23/11/2023 của Giám đốc ĐHQG-HCM bao gồm các thành viên cụ thể như sau: 1) Chủ tịch Hội đồng: PGS.TS Nguyễn Đình Huy, Trường Đại học Bách khoa, ĐHQG-HCM 2) Ủy viên Phản biện: PGS.TS. Trần Tuấn Nam, Trường Đại học Sư phạm Tp. HCM 3) Ủy viên Phản biện: TS. Cao Thanh Tình, Trường Đại học Công nghệ Thông tin, ĐHQG-HCM 4) Ủy viên Hội đồng: PGS.TS. Phan Hoàng Chơn, Trường Đại học Sài gòn, ĐHQG-HCM 5) Ủy viên Hội đồng: TS. Lê Xuân Đại, Trường Đại học Bách khoa, ĐHQG-HCM 6) Ủy viên Hội đồng: PGS.TS. Huỳnh Thanh Công, Ban Khoa học và Công nghệ, ĐHQG-HCM Ủy viên Thư ký: PGS.TS. Võ Ngọc Điều, Trường Đại học Bách khoa, ĐHQG-HCM |
| 11. | Nội dung thực hiện |
– Nội dung 1: Nghiên cứu tìm đường đi ngắn nhât có ràng buộc (chính xác hoặc xấp xỉ) giữa hai điểm trong mặt phẳng, ở đây các ràng buộc là không cắt vật cản Kết quả: Thuật toán hiệu quả tìm đường đi ngắn nhât có ràng buộc giữa hai điểm trong mặt phẳng và thực thi trên máy tính. Vai trò của tính lồi. – Nội dung 2: Ứng dụng các thuât toán trên vào vấn để tìm đường nắm tay (convex rope) cho cánh tay robot và vấn đề robot với tầm nhìn hạn chế tìm dường đi về đích tránh vật cản trong mặt phẳng. Kết quả: Đưa ra thuật toán hiệu quả cho tìm đường nắm tay, cho robot với tầm nhìn hạn chế tìm dường đi tránh số lớp vật cản là hữu hạn các đa giác đơn trong mặt phẳng. – Nội dung 3: Nghiên cứu tìm đường đi ngắn nhât có ràng buộc theo hướng trực giao đã cho và tối ưu theo phương diện diện tích ví dụ như bao lồi trực giao của tập hữu hạn điểm trong mặt phẳng Kết quả: Thuật toán hiệu quả tim các đường đi có ràng buộc theo hướng trực giao ngắn nhất giữa hai điểm và thực thi trên máy tính. |
| 12. | Kết quả |
* Sản phẩm mềm: – Các thuật toán hiệu quả mới tìm đường đi có ràng buộc ngắn nhất giữa hai điểm trong miền đa giác đơn, trên mặt đa diện lồi. – Ứng dụng thuật toán mới cho bàn tay robot cầm vật thể, tìm đường đi ngắn nhất cho robot trên mặt phẳng. * Sản phẩm cứng: Không. * Sản phẩm đào tạo và khoa học: . 03 bài báo (Q1) trên các tạp chí Optimization, Journal of Computational Science, Journal of Global Optimization; . 02 bài báo Q3 trên các tạp chí Discrete Mathematics, Algorithms and Applications, Journal of Convex Analysis. . Đào tạo: 01 thạc sỹ |
| 13. | Hình ảnh giới thiệu kết quả |
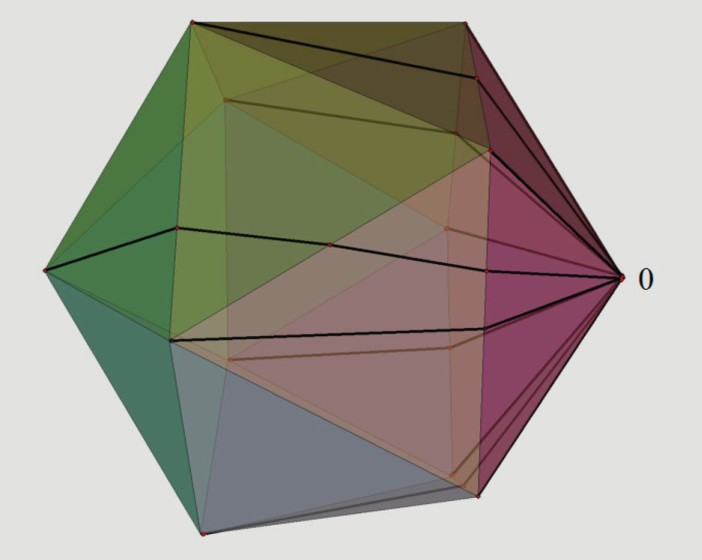
Hình 1:Đường đi tối ưu trên mặt đa diện cho robot từ 1 đỉnh đến các đỉnh
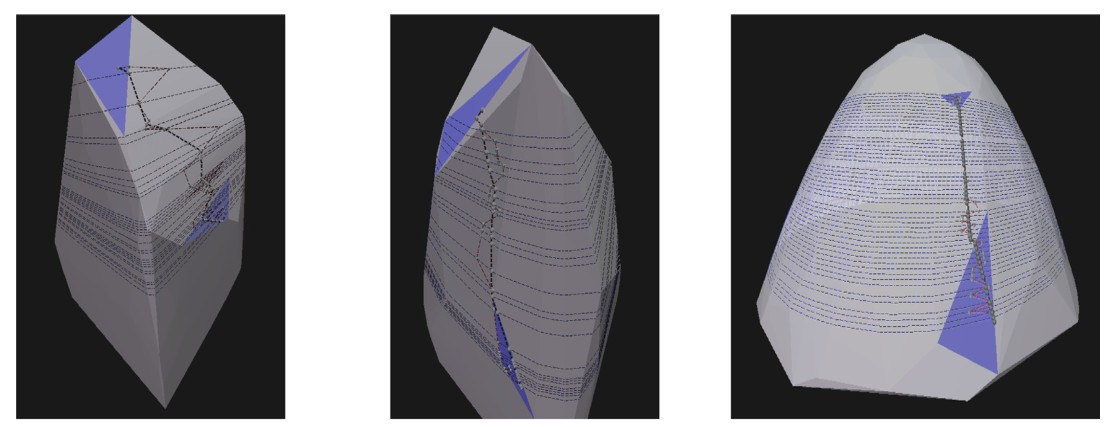
Hình 2: Phương pháp bắn nhiều lần sử dụng cho tìm đường đi tối ưu của robot trên mặt phẳng đa diện
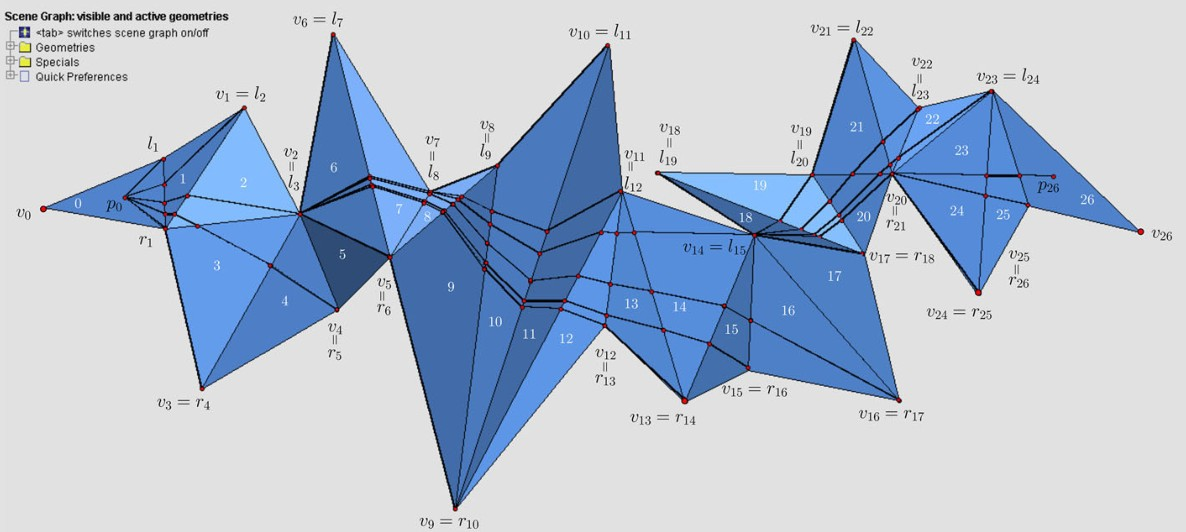
Hình 3: Phương pháp đường định hướng tìm đường đi tối ưu trên mặt địa hình cho robot tự hành |
| 14. | Thông tin liên hệ CNĐT |
thanhan@hcmut.edu.vn Điện thoại: 0983537027 |
| 15. | Liên hệ ĐHQG-HCM | Ban Khoa học và Công nghệ (Phòng 309, NĐH) và Trang điện tử thông tin về hoạt động KH&CN (https://research.vnuhcm.edu.vn/) |
Trường ĐH Bách Khoa, ĐHQG-HCM